题目
给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是排序后的第 k 小元素,而不是第 k 个不同的元素。
示例:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
返回 13。
提示:
你可以假设 k 的值永远是有效的,1 ≤ k ≤ n2 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/kth-smallest-element-in-a-sorted-matrix
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
此笔记参考题解:
思路及算法
从左到右递增,从上往下递增,即matrix[0][0]是最小值,matrix[n-1][n-1]是最大值。我们所需找到的第K小元素必定在[matrix[0][0], matrix[n-1][n-1]]区间内。
至此,有序 + 确定范围 可以使用二分查找
让 left = matrix[0][0] right = matrix[n-1][n-1]
则有 mid = (left + right) >> 1
以下方这个矩阵举例
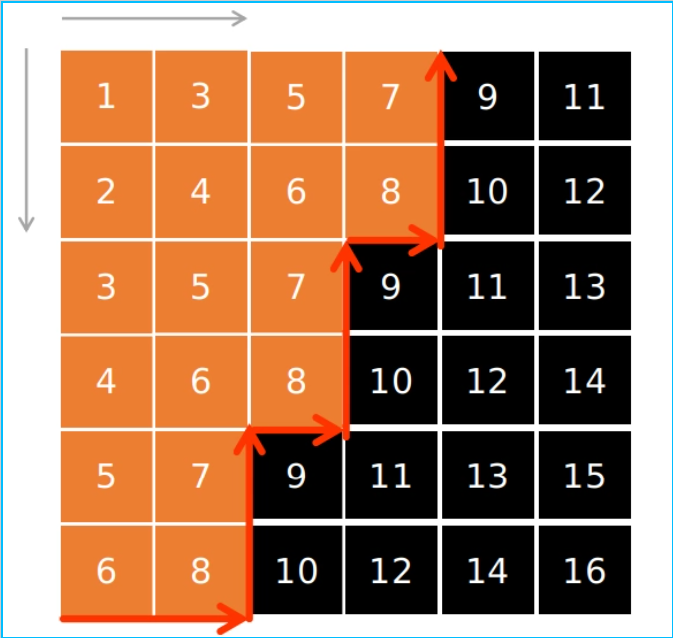
分割矩阵
第一次计算mid = (1 + 16) >> 1 = 8
以mid为界,可以将整个矩阵分割成两个部分,那怎么分?
重要条件 每行和每列元素均按升序排序
从左下角开始的元素开始,不断往右走,当元素小于或等于mid,则此元素及上方所有元素,均是比mid值小的元素。 文字表达不太清楚,看图比较直观。橙色部分都是<=mid的元素

通过mid将矩阵一分为二,则需要我们判断第k小元素在哪一边
这里和常规的二分查找类似,都需要依据mid来判定目标元素在左右的哪一边
但这里又和二分查找又有点区别,就是我们拿什么与什么进行比较
确定查找范围
第一,明白 寻找第k小元素 的区间内元素个数要求
举个例子:1,2,3,4,第3小的元素,那么是3;1,2,2,3,4,同样是第3小的,则是2
由此可知,要找到第k小元素,那么这个区间中至少至少得有k个元素吧!
第二, mid将矩阵分割成两部分,我们简单可以看成较小元素的部分和较大元素的部分,既然寻找第k小元素,结合第一个解释,所以,较小元素部分的元素个数应该是大于等于k的
至此,我们知道是 num(元素较小部分的元素个数) 与 k之间的比较
比较num与k
怎么个比较法?
如果 num >= k ,说明 较小元素部分的范围太大了 需要缩小范围,即「边界收缩」
right = mid
如果 num < k,说明 较小元素部分的范围太小了 需要扩大范围
这里说明下,待查找范围的大小与right有关,而left的作用是查找元素。
即 right将一个大致的范围给定好,然后left在范围内「猜」元素
直接限定范围大小的元素是right吗?不是,是mid。因为我们是以mid为中线,进行分割,所以想扩大范围,就是增大mid值,增大mid意味着增大left或right
left = mid + 1
经过 while left < right 循环,最终跳出循环 return left,left即是答案
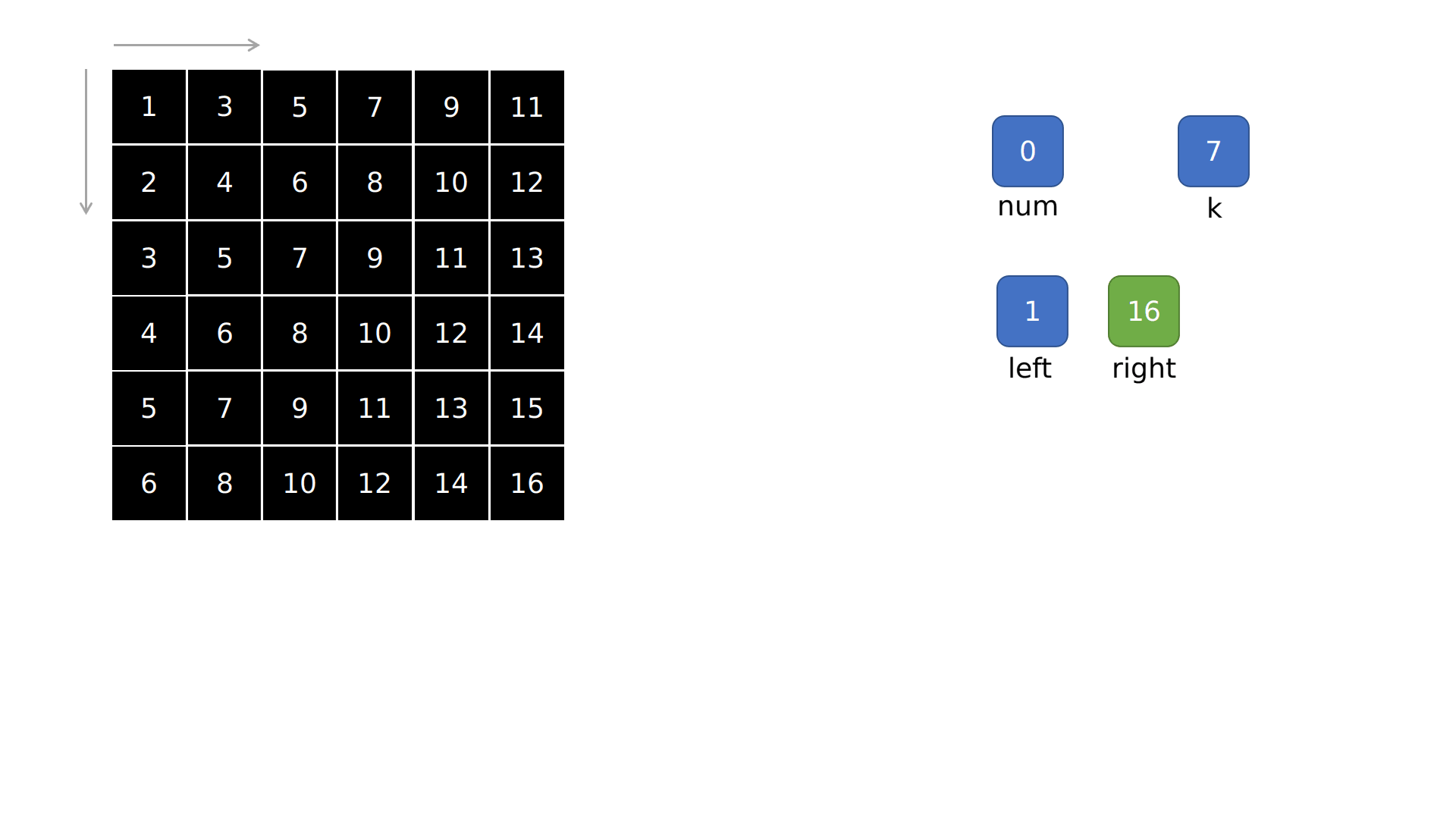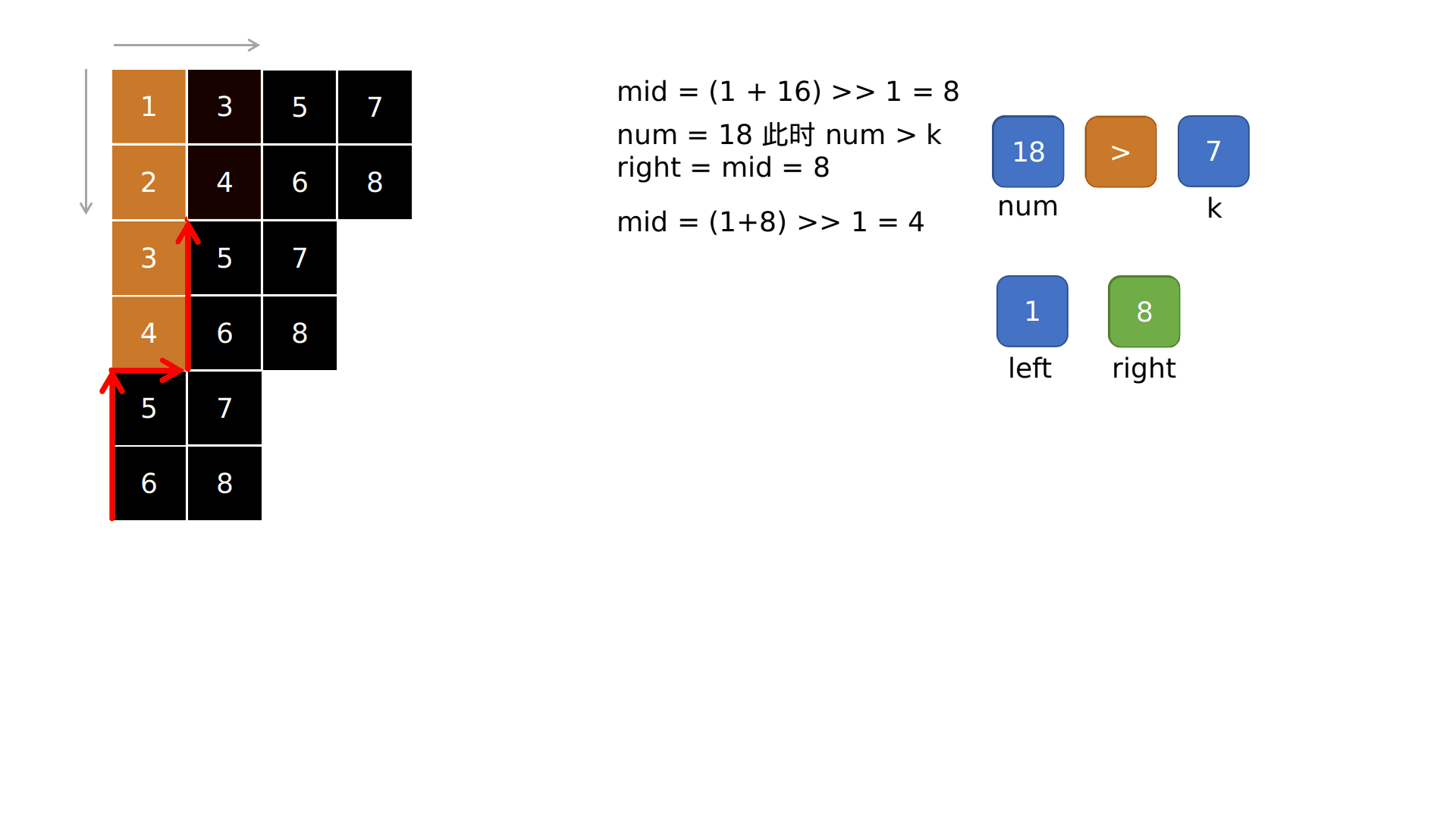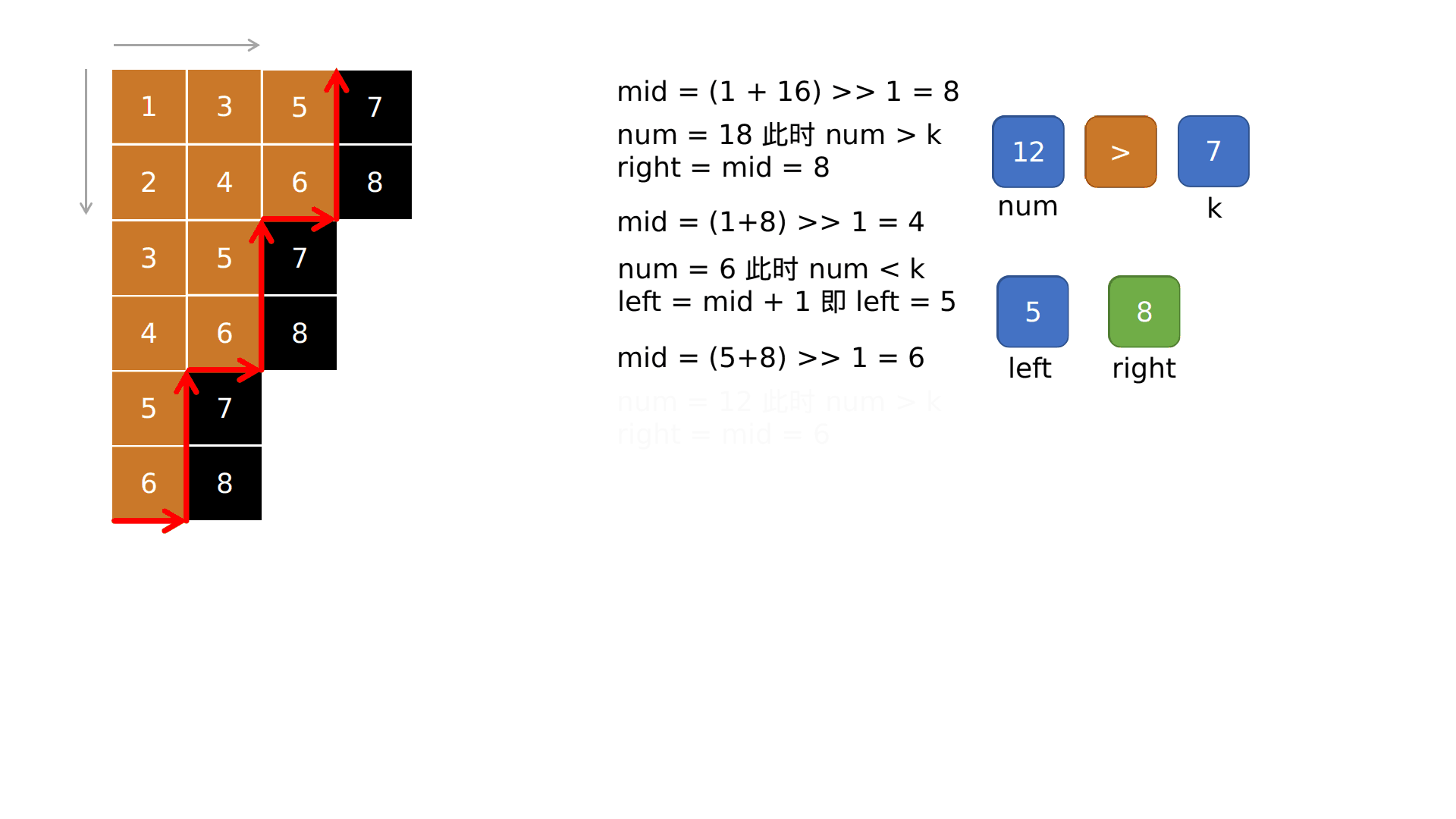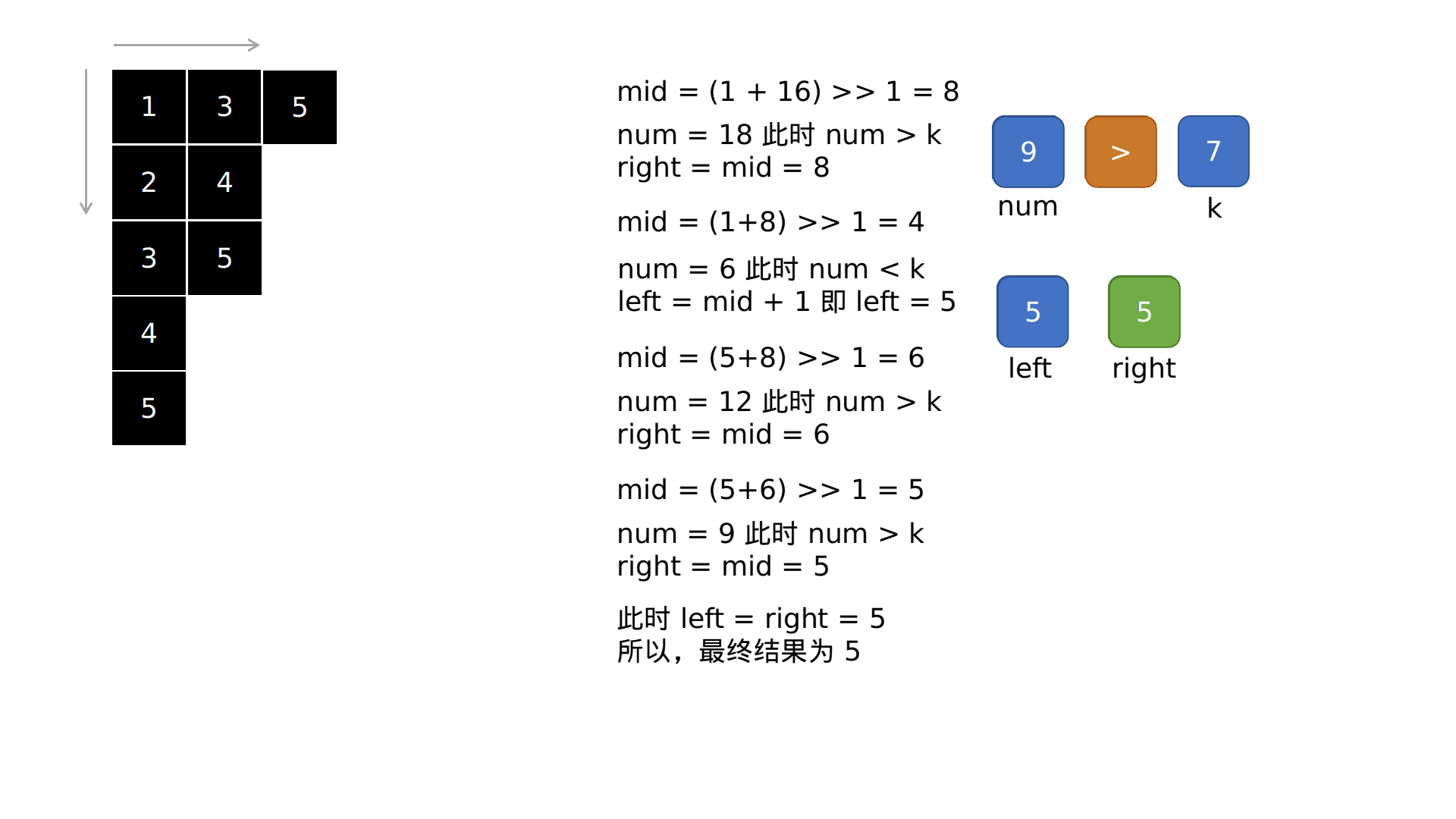
完整代码
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
n = len(matrix)
def check(mid):
"""遍历获取较小元素部分元素总数,并与k值比较"""
i, j = n-1, 0
num = 0
while i >= 0 and j < n:
if matrix[i][j] <= mid:
# 当前元素小于mid,则此函数及上方函数均小于mid
num += i + 1
# 向右移动
j += 1
else:
# 当前元素大于mid,则向上移动,直到找到比mid小的值,或者出矩阵
i -= 1
return num >= k
left, right = matrix[0][0], matrix[-1][-1]
while left < right:
mid = (left + right) >> 1
if check(mid):
# 满足 num >= k,范围太大,移动right至mid, 范围收缩
right = mid
else:
left = mid + 1
return left
问题解释
为什么left就一定是在矩阵中呢?
matrix[0][0]与matrix[n-1][n-1]是存在矩阵中,而计算出来的mid,可能不在矩阵中,也就意味后续相关的left与right也可能不在矩阵中,那么为什么偏偏left就在矩阵中而且还是正确答案呢?
先来看一个简单的矩阵示例:
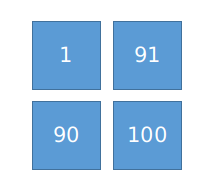
要求:找到第2小的元素
在这个矩阵中,第一次mid计算值为50(不在矩阵中),以50为分割,得到的num为1
在循环中,num 一直小于k, 则left 一直在做 mid + 1,最终加到80的时候,mid = (80 + 100) / 2 = 90,至此使得num为2,此时num=k,即right = mid = 90,left继续做mid+1,当加到90时,left = right,退出循环,返回left,即90
通过这个简单的矩阵,就知道 第k小的值不是直接算出来的,而是「猜」出来的,二分查找就是在不断缩小范围并猜值
回到问题,为什么left就一定是在矩阵中呢?
上面的示例,退出循环时,必定有left=right,返回left即返回right,所以right的值是最终答案
好的,那么right的值怎么来滴,由right=mid可知,mid决定right
所以,mid就是最终答案(有特例,比如[[-5]]), 这里只是笼统的认为,方便理解
(left + right) / 2 决定了mid, left的变换是因为num<k
因为left在不停的失错,直到使得mid的值,可以满足num>=k
这也说明了,此方法只适用于整数矩阵,如果是小数就不行了,因为每次试错的最小增量是1